Boxplots

Note: If you are viewing this article within the Help Desk widget from within the course textbook, we recommend opening the article in a new tab with the button in the top right corner (as seen below) so that the images will be easier to see.

A boxplot is a visualization of the five-number summary of a distribution, plus outliers. (For more information on the five-number summary see this article: five-number summary).

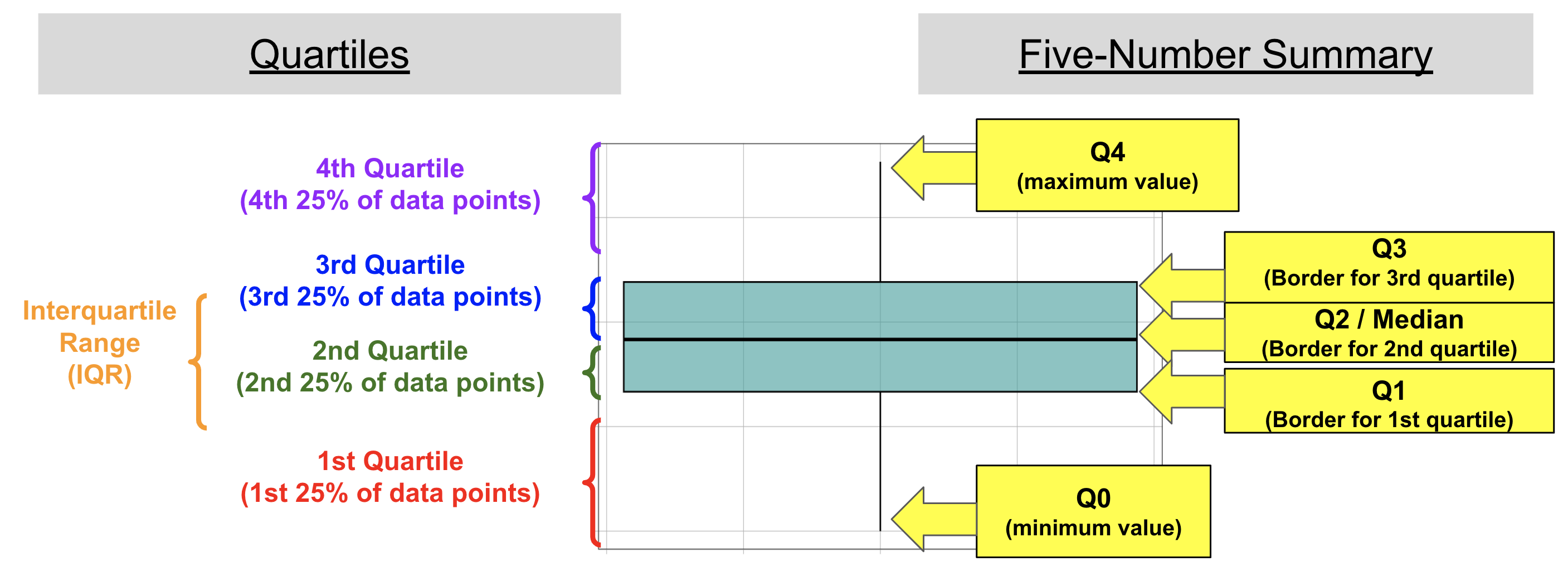
What are the boxes and whiskers in a boxplot?

We use boxplots to show the distribution of data mainly through four quartiles. The boxplot has two whiskers (first quartile, and fourth quartile), and two smaller boxes (second quartile, and third quartile). The two small boxes together make a larger central box, and the range of that box is known as the IQR or interquartile range. 

The IQR captures the middle half of the data, or the data excluding the top 25% of data and bottom 25% of data. Q1 to the Median (middle black line) represents data that fall within the second quartile, and the Median to Q3 represent the third quartile of the data.  

The length of the box or whiskers shows you how spread out those values are, but each quartile contains an equal number of data points, so even if one whisker is longer than the other it does not mean there are more data points in that whisker.  If there are any outliers in a distribution, they will appear as separate data points beyond the whiskers of the boxplot.                                                                                                        

Example

In the boxplot below, we can see the distribution of the following values (n = 12): 

3, 4, 5, 8, 10, 18, 19, 19, 20, 22, 24, 29 

We have 12 values, so if we include the dots for each value along with the boxplot (using the gf_jitter() function) we can see that each quartile contains 3 points. We can also see that the second and fourth quartiles have more spread than the other two quartiles

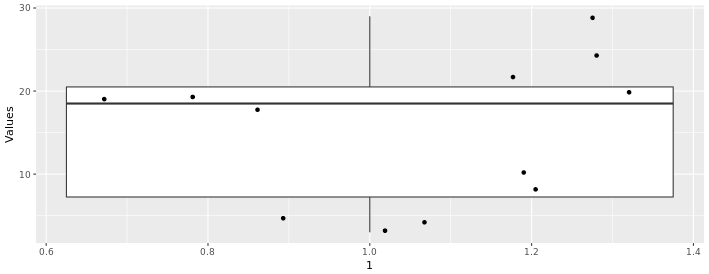
Boxplots and Outliers

If we take the same distribution above and just change the last two values from 24 and 29, to 55 and 60:

3, 4, 5, 8, 10, 18, 19, 19, 20, 22, 55, 60

We get the boxplot below:

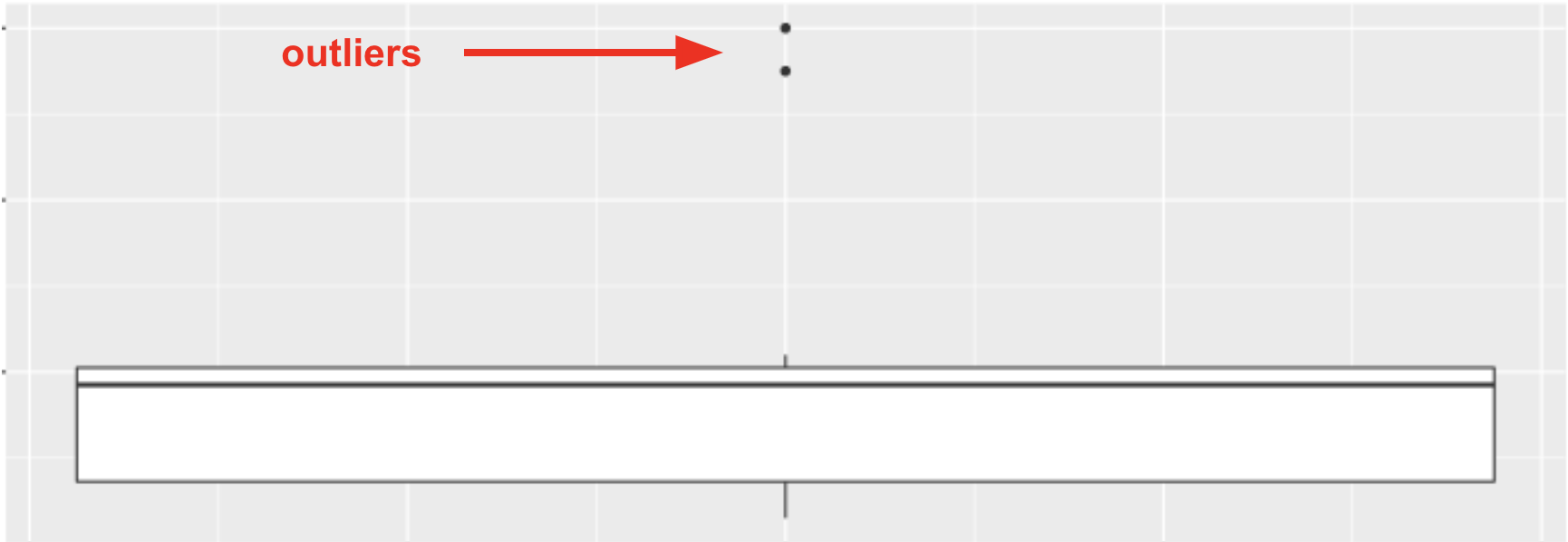
The points that appear on a boxplot are the outliers. If they appear above the top whisker, they are outliers because R has checked whether these values are greater than Q3+1.5*IQR. If they appear below the bottom whisker, they are outliers because their values are smaller than Q1−1.5*IQR. When there are outliers, the end of the whiskers depicts the max or min value that is not considered an outlier.

What types of variables are used in a boxplot?

Also note that the boxplots above are displaying the distribution for a single, quantitative variable, and that the horizontal width of the boxes (along the x-axis, in this case) does not mean anything. If we wanted to compare boxplots across the groups of a categorical variable, we could do so, as seen below. In this case, we can compare the distribution textbook cost (a quantitative variable) for four different academic fields (a categorical variable). Again, the horizontal width of the boxes is not meaningful.

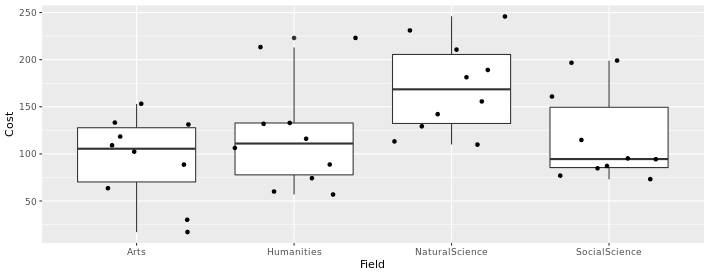
Switching the variables on each axis

We can also switch the variables for the axes of our boxplots if we prefer to view them that way, by switching the variables around the ~ in our code. For instance, the code below produces the boxplots above:

gf_boxplot(Cost ~ Field, data = TextbookCosts) %>% gf_jitter()

But if we switch around the variables, like so:

gf_boxplot(Field ~ Cost, data = TextbookCosts) %>% gf_jitter()

We get the visualization below. Notice that now the cost of the textbooks is along the x-axis now, and the groups (Field) run along the y-axis. When our boxplots are displayed in this format, now it is the vertical width of the boxes that is not meaningful.

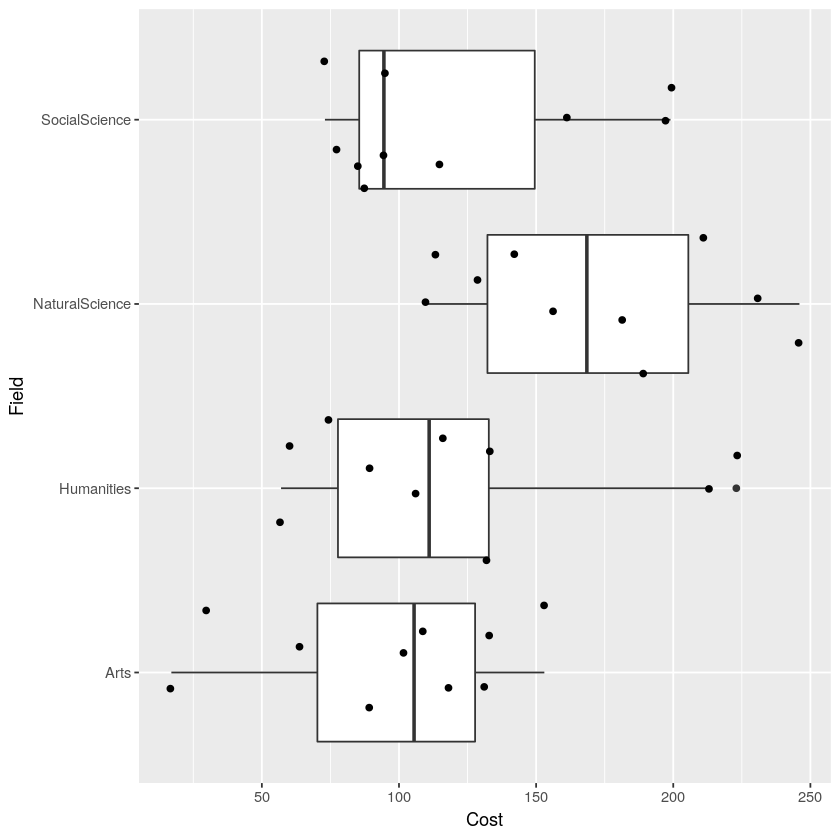
• Related Articles

• sample distribution

  When sampled data—units that were selected and measured—are shown in such a way where we can see patterns of variation (such as shape, center, and spread); sample distributions can be seen in visualizations such as histograms, boxplots, etc. but also ...

• gf_jitter()

  The gf_jitter() function will generate a jitter plot. A jitter plot is a point plot (similar to a scatter plot, such as gf_point()) but the points are moved slightly ("jittered") so that they do not overlap as much. This can help make it easier to ...

• gf_boxplot()

  The gf_boxplot() function will generate a boxplot (also known as a box and whiskers plot). A boxplot splits the data into quartiles, where each whisker and each half of the box contains 25% of all the observations. They are helpful for visualizing ...

• Five-Number Summary

  The 5-number summary is a way to describe the spread of a distribution around a median. If we start by sorting the values from smallest to largest, then chunk our data into quartiles (four equal groups of data points) we can get the five-number ...